Comparison of the Empirical Method and the Classical Method
| Event | Frequency |
| 3 Boys | 8 |
| 3 Girls | 12 |
| 2 Boys + 1 Girl | 11 |
| 2 Girls + 1 Boy | 9 |
Let's compare both the classical and empirical methods. Forty families with three children each were surveyed to determine the number of boys and girls in each family. This table displays the results.
In comparing, we can see that the two are slightly different. Generally speaking, as the number of repetitions increases, the empirical probability becomes closer to the classical probability.
Empirical Method
Classical Method
First, we will use the empirical method to estimate the probability of a family having three boys.
The empirical probability of Event E = "three boys" is `P(E) = 8/40=1/5=.20`.
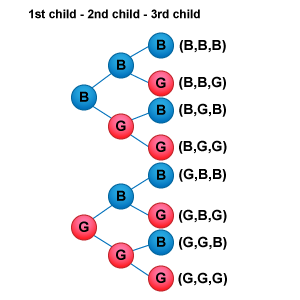
To compute using the classical method to estimate the probability of a family having three boys, we count the number of outcomes in the sample space. We begin by identifying the sample space.
S = {(B,B,B), (B,B,G), (B,G,B), (B,G,G), (G,B,B), (G,B,G), (G,G,B), (G,G,G)}, so N(S) = 8.
For Event E = "three boys" = {(B,B,B)}, we have N(E) = 1. Because the outcomes are equally likely, the probability of E is `P(E) = (n(E)) / (n(S)) = 1/8 = .125`.



